

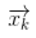
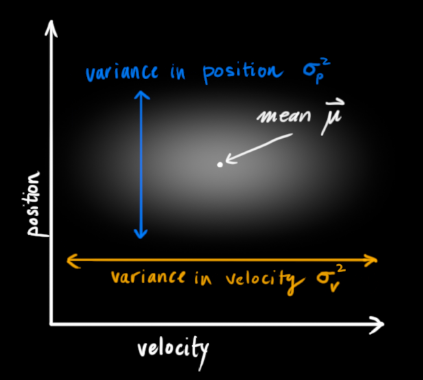
,表示位置和速度:
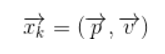

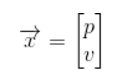
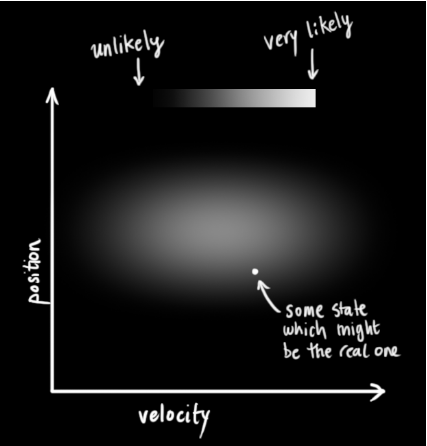
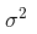
,表示不确定性。
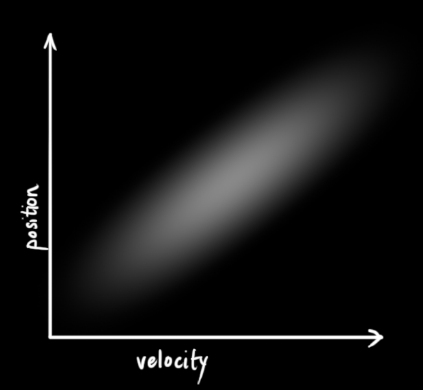
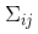
表示第 i 个和第 j 个状态变量之间的相关度。(你可能已经猜到协方差矩阵是一个对称矩阵,这意味着可以任意交换 i 和 j)。协方差矩阵通常用“
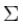
”来表示,其中的元素则表示为“
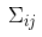
”。
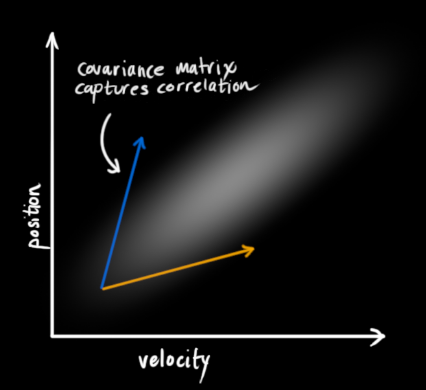
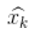
(即均值,其它地方常用 μ 表示),以及协方差矩阵
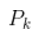
。
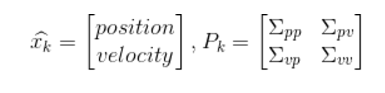
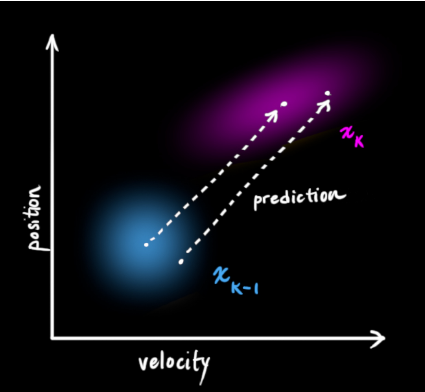
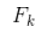
来表示这个预测过程:
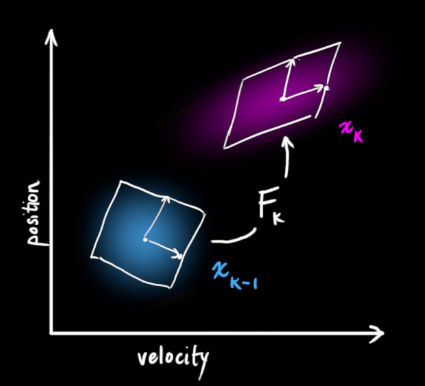
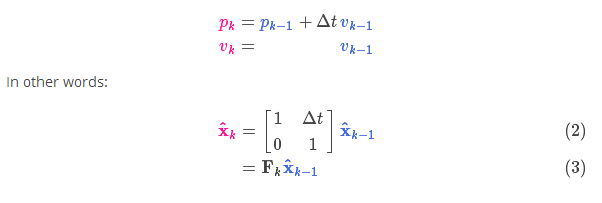
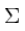
会怎样变化呢?很简单,下面给出公式:
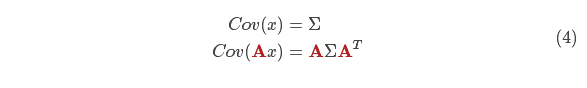
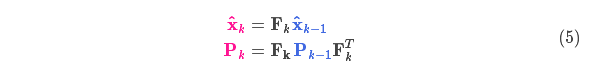
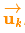
来表示,将它加到我们的预测方程中做修正。
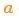
,根据基本的运动学方程可以得到:
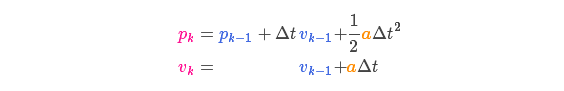
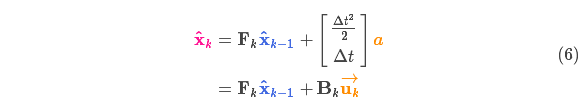
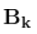
称为控制矩阵,
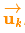
称为控制向量(对于没有外部控制的简单系统来说,这部分可以忽略)。让我们再思考一下,如果我们的预测并不是100%准确的,该怎么办呢?
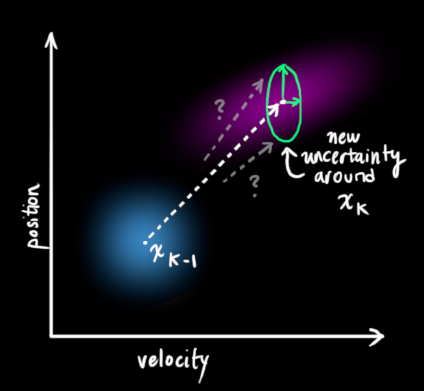
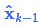
的每个状态变量移动到了一个新的服从高斯分布的区域,协方差为
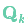
。换句话说就是,我们将这些没有被跟踪的干扰当作协方差为
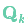
的噪声来处理。
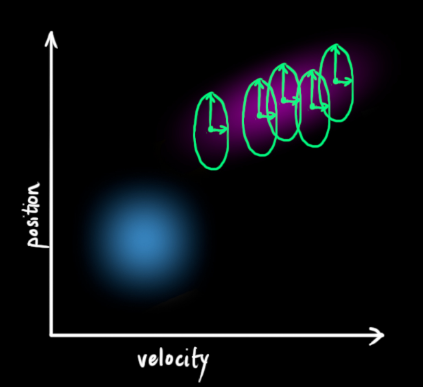
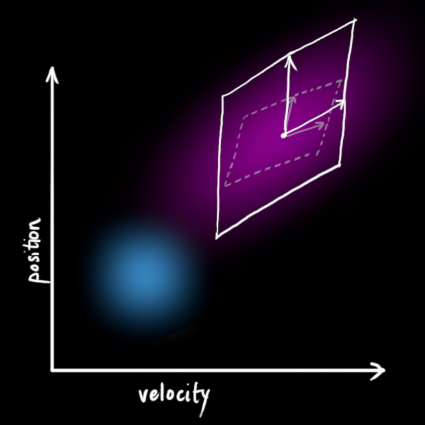
得到扩展的协方差,下面给出预测步骤的完整表达式:
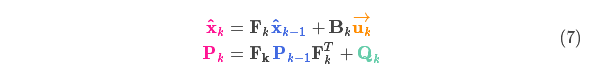
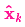
和
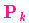
来表示。如果再结合传感器的数据会怎样呢?
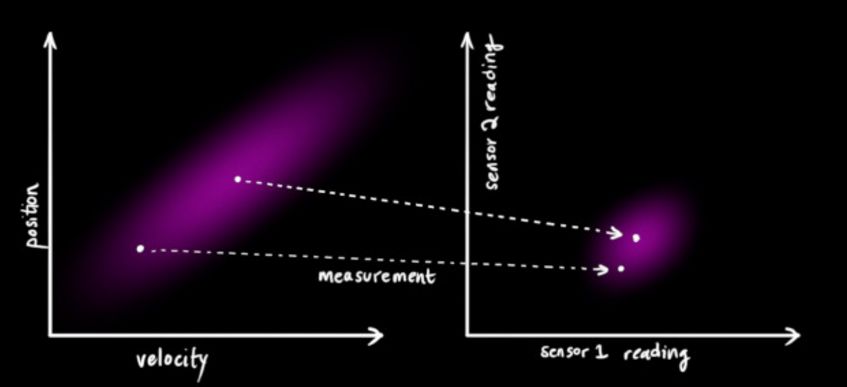
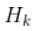
来表示传感器的数据。
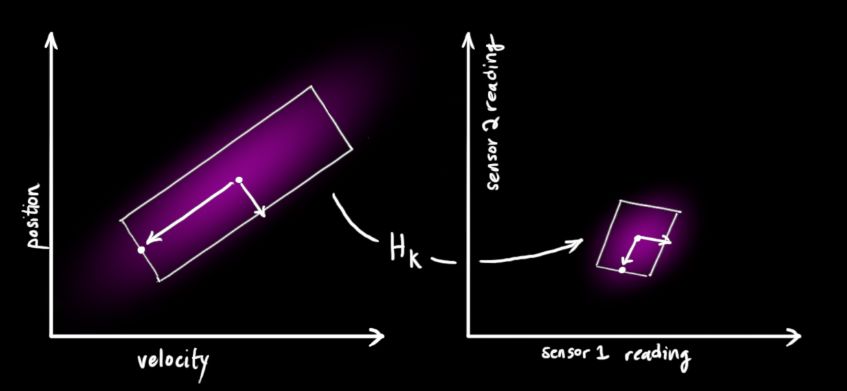
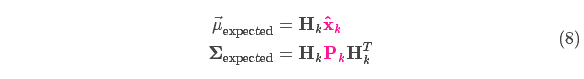
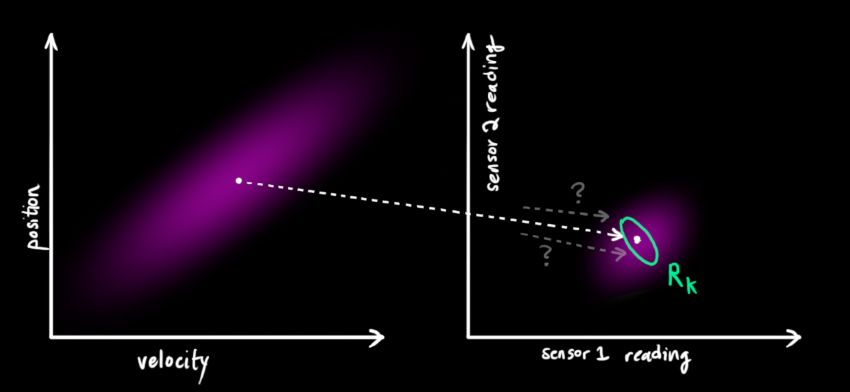
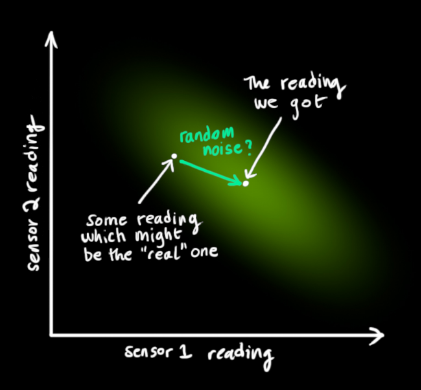
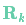
表示,该分布的均值就是我们读取到的传感器数据,称之为

。
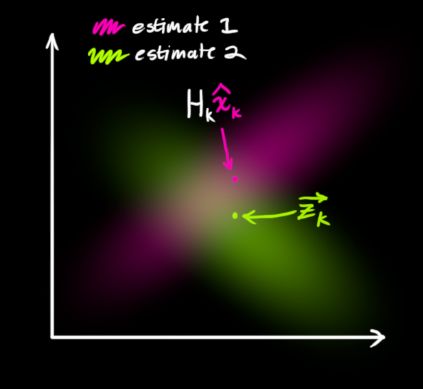
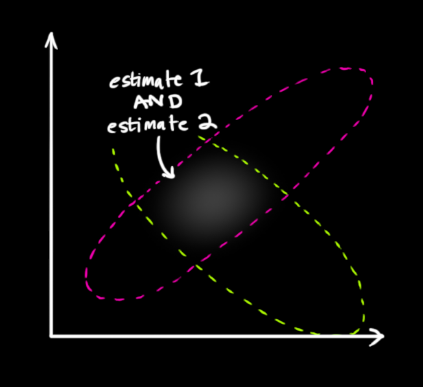
,有两种情况:(1)传感器的测量值;(2)由前一状态得到的预测值。如果我们想知道这两种情况都可能发生的概率,将这两个高斯分布相乘就可以了。
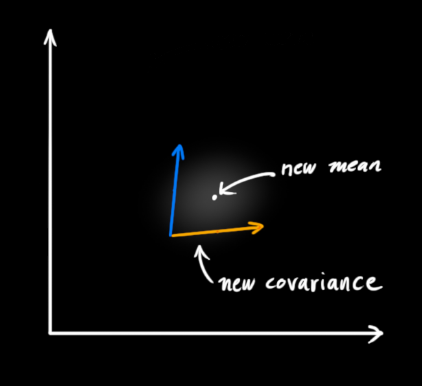
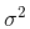
和 μ 的高斯曲线可以用下式表示:
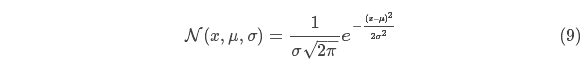
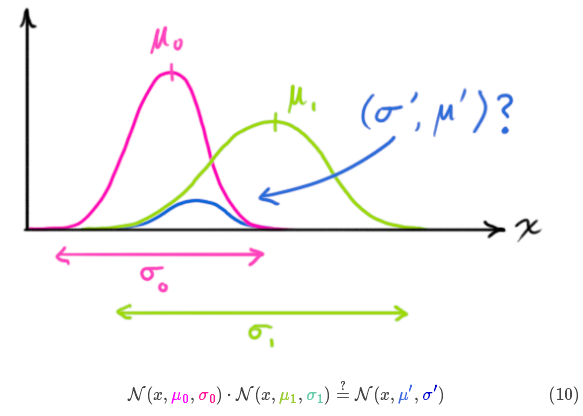
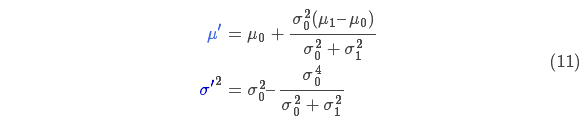
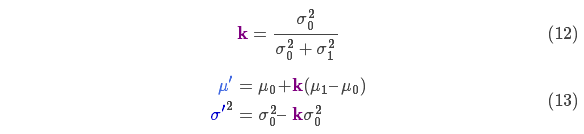
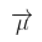
表示每个维度的均值,则:
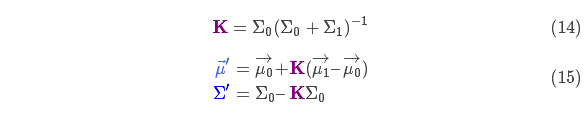
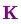
称为卡尔曼增益,下面将会用到。放松!我们快要完成了!
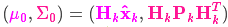
,和测量部分
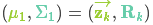
,将它们放到式(15)中算出它们之间的重叠部分:
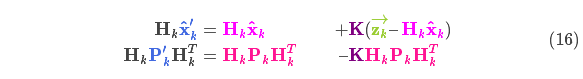

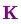
里面包含了
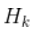
)将其约掉,再将式(16)的第二个等式两边同时右乘矩阵
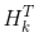
的逆得到以下等式:
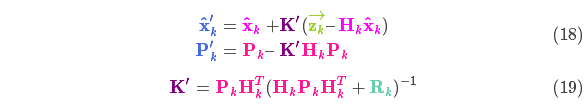
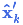
就是新的最优估计,我们可以将它和

放到下一个预测和更新方程中不断迭代。
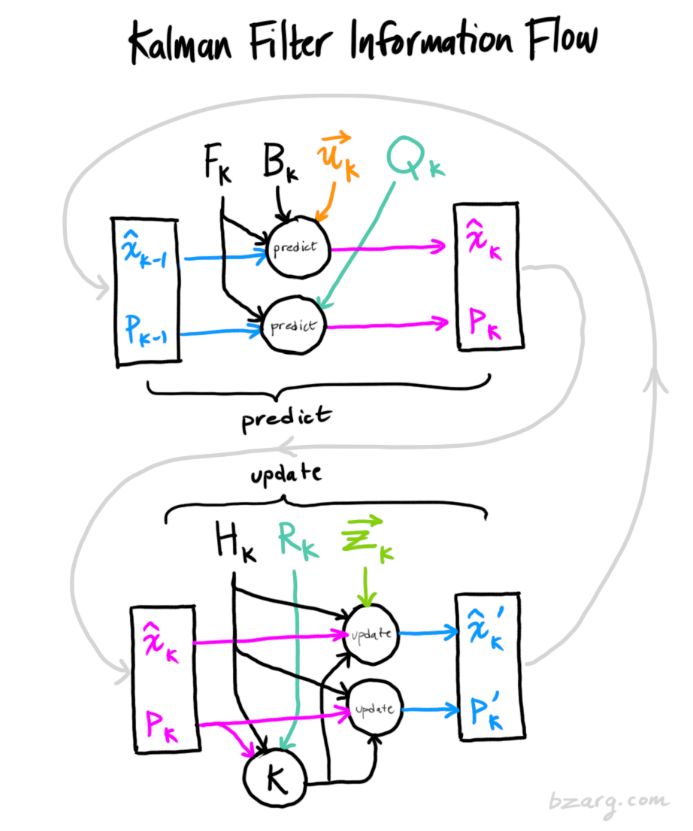
关注微信公众号『玩转嵌入式』,后台回复“128”获取干货资料汇总,回复“256”加入技术交流群。
精彩技术文章推荐
|
01 |头文件中,#include使用引号“”和尖括号<>有什么区别? |
|
02 |数据安全很重要,如何保证数据的有效性?嵌入式常用的校验算法介绍 |
|
03 |C语言,动态展示经典排序算法 |
|
04 |插入排序:最直观的排序算法 |

免责声明:本文内容由21ic获得授权后发布,版权归原作者所有,本平台仅提供信息存储服务。文章仅代表作者个人观点,不代表本平台立场,如有问题,请联系我们,谢谢!